Linear Discriminant Analysis

LDA is closely related to PCA as it is linear.

• PCA, the transformation is baed on minimizing mean square error between original data vectors and data vectors that can be estimated fro the reduced dimensionality data vectors

• LDA, the transformation is based on maximizing a ratio of “between-class variance” to “within-class variance” with the goal of reducing data variation in the same class and increasing the separation between classes.

Here is the graphic intuition:

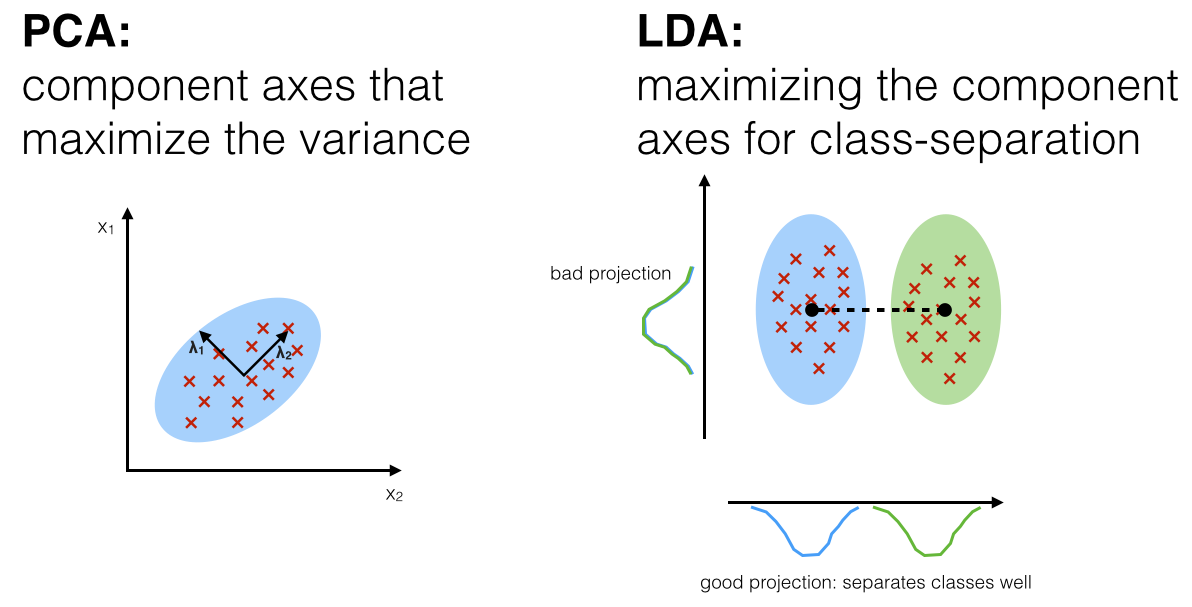
Goals:

1. Obtain a scalar y by projecting the samples X onto a line:

1. Find $\beta^{*}$ to maximize the ratio of “between-class variance” to “within-class variance”.

1. Two classes problem

1.1. Head the problem

Mean-class vector: Mean vector of each class with its projection

Between-class variance: a measure of separation between two classes is to choose the distance between the projected means, which is in y-space

Within-class variance: Variance of the elements of the $k$-th class relative to its mean

Objective function: We are looking for a projection where examples from the class are projected very close to each other and at the same time, the projected means are as farther apart as possible. Naturally: $J(\beta) = \frac{(\hat{u}_{2} - \hat{u}_{1})^{2}}{\hat{s}_{1}^{2} + \hat{s}_{2}^{2}}$

1.2. Transform the problem

Goal: We need to express $J(\beta)$ as a function of $\beta$:

Scatter in feature space-x: Measure of how the points are spread away from the mean of a given class

Within-class scatter matrix: Total scatter of all classes

Between-class scatter matrix: Distance Matrix of the class means $S_{B} = (u_{2}-u_{1})(u_{2}-u_{1})^{T}$

Objective function reformulation: With these notations, we obtain:

1.3. Solve the problem

Fisher’s linear discriminant: By setting the derivative to zero we obtain:

2. Multi class

2.1. Objective function

We obtain similarly (proof):

Goal: seek the projection matrix $\Theta^{*}$ that maximize this ratio.

Fisher’s criterion: is maximized when the projection matrix $\Theta^{*}$ is composed of the eigenvectors of:

and under the assumptions that $S_{W}$ is

• Non-singular matrix
• Invertible

LDA and dimensionality reduction: Noticed that, there will be at most $(C−1)$ eigenvectors with non-zero real corresponding eigenvalues $λ_{i}$. This is because $S_{B}$ is of rank $(C − 1)$ or less. So we can see that LDA can represent a massive reduction in the dimensionality of the problem.