The scale free property
Mis à jour :
Hubs are encountered in most real networks. They represent a signature of a deeper organizing principle that we call the scale-free property.
Intrinsically linked to the degree distribution of real networks, which allows us to uncover and characterize scale-free network and further - from communities to spreading processes.
Power Laws and Scale-Free Networks
Most real networks degree distribution do not have the expected Poisson distribution. A log-log plot of real networksreveal that most degree distribution are well approximated with:
Definition (Power law distribution): and its degree exponent $\gamma$:
Definition (Scale-free network): is a network whose degree distribution follows a power law.
Note: In undirected networks, we distinguish:
Discrete Formalism: $p_{k}=Ck^{-\gamma} = \frac{k^{-\gamma}}{\zeta(-\gamma)}$
Continuous Formalism:
80/20 Rule: In real networks, most links points to a small amount of nodes. These nodes are hubs.
Hubs
The main difference between a random and a scale-free network comes in the tail of the degree distribution.
| Distribution | Max hub size | Hub presence | Complexity | |
|---|---|---|---|---|
| Random Networks | Exponential | $k_{max} = k_{min} + \frac{ln(N)}{\gamma}$ | Unlikely | $O(log(n))$ |
| Random Networks | Poisson | Slower than log(n) | Unlikely | $\approx O(log(n))$ |
| Scale-free networks | Power | $k_{max} = k_{min} N^{\frac{1}{\gamma-1}}$ | Naturally | $O(N^{\frac{1}{\gamma-1}})$ |
The Meaning of Scale-Free
Terminology (scale-free): rooted in the theory of phase transitions (statistical physics) that extensively explored power laws in the 1960s and 1970s.
Definition ($n$-th moment): of the degree distribution is defined as
Interpretations:
- The first moment is the average degree $\langle k \rangle$
- The second moment $\langle k^{2} \rangle$, helps us calculate the variance $\sigma^{2} = \langle k^{2} \rangle − \langle k^{2} \rangle$, measuring the spread in the degrees.
- The third moment $\langle k^{3} \rangle$ determines the skewness of a distribution, telling us how symmetric is $p_{k}$ around the average $\langle k \rangle$
Property (Power law n-th moment):
Notes:
- k_{min} is typically fixed
- k_{max} increases with the system size
Key takeaway: The asymptotic behavior depends on \gamma.
- $n \leq \gamma−1 \Rightarrow n$-th moment is finite.
- $n > \gamma−1 \Rightarrow n$-th moment diverges.
Note: Most scale-free networks the degree exponent γ is between 2 and 3.
Scale?
- Random Networks: Have an intrinsic scale $\langle k\rangle$
- Scale-free Networks: Lack a scale (infinite variance if $\gamma < 3$) and for a randomly chosen node, we do not know what to expect.
Note: This divergence is the origin of some of the most intriguing properties of scale-free networks, from their robustness to random failures to the anomalous spread of viruses.
Universality principle
The power law approximates well lots of real networks. It is this diversity that prompts us to call the scale-free property a universal network characteristic.
This prompts us to address several issues pertaining to plotting and fitting power laws:
Plotting the Degree Distribution:
- Perform $log_{10}-log_{10}$ plot
- Use logarithmic binning
- Use Cumulative Distribution
Notes:
- Careful! $p_{k} = 0$ or $k=0$ are not shown on a log-log plot as $log(0)=-\infty$.
- Logarithm binning ensure that each bin has a comparable number of nodes (linear binning does not).
- Cumulative distribution enhances the statistical significance the high-degree region.
Some recurring features:
- Low-degree saturation: Its signature is a flattened $p_{k}$ for $k < k_{sat}$
- High-degree cutoff: rapid drop in $pk$ for $k > k_{cut}$, ( fewer high-degree nodes than expected in a pure power law)
Alternative fitting procedure:
The presence of such cutoffs indicates the presence of additional phenomena that need to be understood.
Measuring the Degree Exponent
A quick estimate of the degree exponent can be obtained by fitting a straight line to pk on a log-log plot.Yet, this approach can be affected by systematic biases, resulting in an incorrect γ. The statistical tools available to estimate γ are discussed in ADVANCED TOPICS 4.C.
The shape of $p_{k}$
ADVANCED TOPICS
Ultra-small Property
Do hubs affect the small world property?
distances in a scale-free network are smaller than the distances observed in an equivalent random network.
dependence of the average distance \langled〉 on the system size N
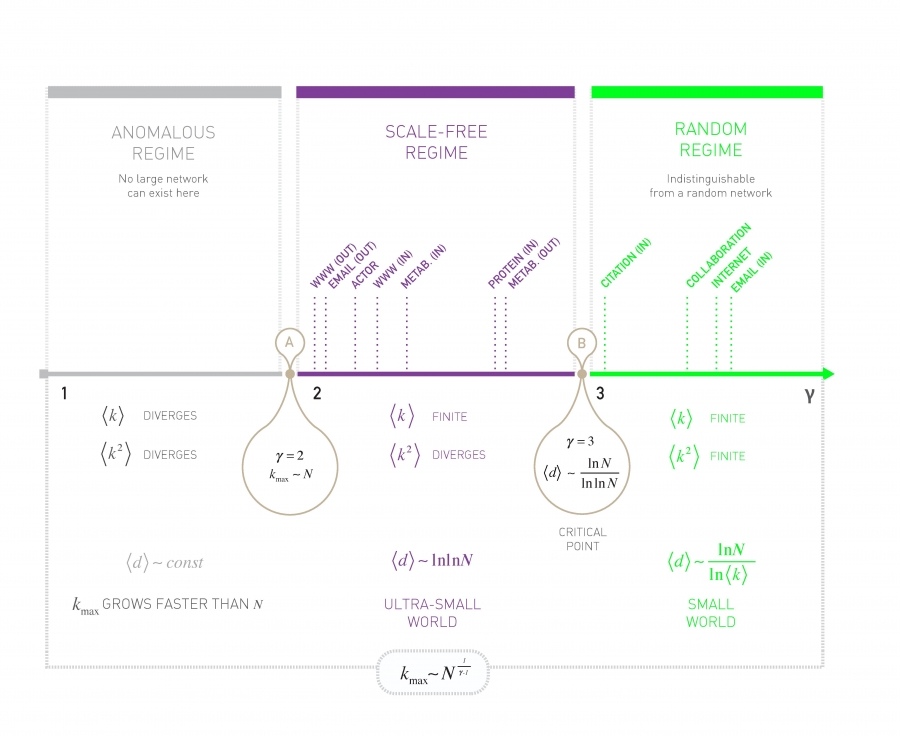
Anomalous Regime ($\gamma = 2$)
biggest hub grows linearly with the system size, i.e. kmax ~ N
hub and spoke configuration in which all nodes are close to each other because they all connect to the same central hub. In this regime the average path length does not depend on N.
Ultra-Small World (2 ‹ γ ‹ 3)
average distance increases as lnlnN (slower growth than the lnN derived for random networks) hubs radically reduce the path length (linking to a large number of small-degree nodes, creating short distances between them)
Critical Point (γ = 3)
theoretical interest, as the second moment of the degree distribution does not diverge any longer
At this critical point the lnN dependence encountered for random networks returns. Yet, the calculations indicate the presence of a double logarithmic correction lnlnN [29, 31], which shrinks the distances compared to a random network of similar size.
Small world
$\langle k^{2} \rangle$ is finite and the average distance follows the small world result derived for random networks. While hubs continue to be present, for γ > 3 they are not sufficiently large and numerous to have a significant impact on the distance between the nodes.
Result: The more pronounced the hubs are, the more effectively they shrink the distances between nodes
In summary the scale-free property has several effects on network distances:
- Shrinks the average path lengths
- Changes the dependence of 〈d〉 on the system size
- Only for γ › 3 we recover the lnN dependence
The Role of the Degree Exponent
Generating Networks with Arbitrary Degree Distribution
Goal: Generate networks with an arbitrary p_{k}

Laisser un commentaire