Louis de Vitry

Louis de Vitry

Mathematics and computer science enthusiast

Words representation

20 minute de lecture

Mis à jour :

Word2Vec rocks!

  1. Historical perspective
  2. What is skipgram?
  3. word2vec in python!
  4. Improve word2vec
  5. Experiments
  6. Recent breakthroughs in litterature

1. Historical prespective

1.1. Bag of Word

When it comes to supervised learning in general, the goal can most often than not be boiled down to finding a parametrized model $f_{\theta}$ that explains best some annotated data $(X, Y) = {(x_{i}, y_{i})}_{i=1}^{N}$. And usually, the parameters $\theta$ are learnt to satisfy:

where $\phi$ is some feature extraction function and $R$ some regularization. Altogether, it simply means that the model parameters $\theta$ are learnt to map at best a representation $\phi$ of the data $X$ to our targets $Y$!

The missing piece: In NLP, the first major feature representation $\phi$ is is the Bag-of-word (BOW), which is credited to Gerard Salton (see this The Most Influential Paper Gerard Salton Never Wrote for more details).

Example: For the sentence "John likes to watch movies. Mary likes movies too." , it works by counting each words and storing the results with dictionaries:

bag_of_words = {
  "John":1,
  "likes":2,
  "to":1,
  "watch":1,
  "movies":2,
  "Mary":1,
  "too":1
}

In practice though, storing dictionaries is quite inefficient, so one should use the hashing trick to simplify the implementation of bag-of-words models and improve scalability. In NLP, the simplest hashing is the document-term matrix, whose columns are the words and the rows are the documents. It is a sparse matrix of size $N \times V$, with $V$ being the size of our vocabulary and it looks quite like this:

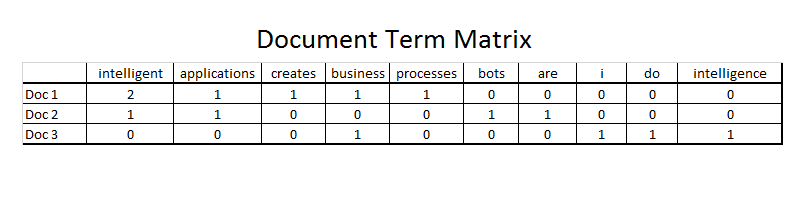
Document term matrix

Drawbacks of BoW: This representation is nonetheless limited because it does not account for the word order, multi-word expressions and finally because words are discrete.

TODO: Give examples if possible

1.2. Pre deep learning era

Before the first successes of Deep Learning in NLP, the common procedure to build a representation $\phi$ was based on combinations of the following building blocks:

  1. Intrinsic features are based on the information contained in the word itself:
    • Document-term matrix defined above
    • Stemmed Word and Lemmatized Word generate the root form of the inflected words but the difference is that stem might not be an actual word whereas, lemma is an actual language word.
    • Informations from lexical data-bases (dictionaries, hypernyms, synonyms,….)
    • POS tags is the process of marking up a word in a text (corpus) as corresponding to a particular part of speech, based on both its definition and its context. A simplified form of this is commonly taught to school-age children, in the identification of words as nouns, verbs, adjectives, adverbs, etc.
  2. Extrinsic features are based on the surrounding words:
    • Co-occurrence matrix: For a given word, we count their surrounding words (rolling window of +/- 5 words) and store the results in a matrix of size $V \times V$.
    • Weighted Co-occurrence matrix: The raw co-occurence matrix is unnormalized in the sense that most frequent pairs are given more interest. This issue can be solved by using point-wise mutual information on every pair.
  3. Compress the sparse features with Latent Semantic Analysis. The basic idea is to use the eigenvectors obtained by a SVD to map term to documents.

Afterwards, the encoded data $\phi(X)$ is fed to a Machine Learning algorithm (usually a Support Vector Machine).

Note:

  • In some cases, the results of the LSA is the finality.
  • There are a lot of variations and additional precisions behind these techniques. I just give an outline here.

1.3. The promises of Deep Learning

In many fields like Deep Learning proved to be really useful in producing a higher-level representation of the input data. Therefore, the process of constructing a feature representation $\phi$ can be done by learning them with a Neural Language model. This idea was first introduced in 2003 by a paper called A Neural Probabilistic Language Model written by Bengio et al. This was further extended ten years later with two central papers written by Mikolov et al. that made what we know as word2vec work:

  1. Efficient Estimation of Word Representations in Vector Space
  2. Distributed Representations of Words and Phrases and their Compositionality

We will build our word2vec based on those papers. Two models exist for computing word2vec, and according to Mikolov, the main differences are:

Skip-gram: works well with small amount of the training data, represents well even rare words or phrases.

CBOW: several times faster to train than the skip-gram, slightly better accuracy for the frequent words

Motivated by the above reasons and others described in this Q&A, I chose the SkipGram architecture. And much like manually crafted extrinsic features, these techniques are also motivated by the distributional hypothesis which basically states that in order to understand a word, one should see how it is used. This passage illustrates it best:

” The placing of a text as a constituent in a context of situation contributes to the statement of meaning since situations are set up to recognize use. As Wittgenstein says, ‘the meaning of words lies in their use.’. The day-to-day practice of playing language games recognizes customs and rules. It follows that a text in such established usage may contain sentences such as ‘Don’t be such an ass !’, ‘You silly ass !’, ‘What an ass he is !’ In these examples, the word ass is in familiar and habitual company, commonly collocated with you silly-, he is a silly-, don’t be such an-. You shall know a word by the company it keeps ! One of the meanings of ass is its habitual collocation with such other words as those above quoted. Though Wittgenstein was dealing with another problem, he also recognizes the plain face-value, the physiognomy of words. They look at us ! ‘The sentence is composed of words and that is enough’”

2. What is SkipGram

TL; DR: “[Consinuous SkipGram predicts] the current word based on its context, and tries to maximize classification of a word based on another word in the same sentence. More precisely, we use each current word as an input to a log-linear classifier with continuous projection layer, and predict words within a certain range before and after the current word.” - Original paper

In this section, we explain the inner-workings of the Skip Gram model in its intricate details. Specifically, we answer the questions:

  • What is learnt?
  • How does it learn?
  • How to learn even faster?

2.1. What is learnt?

While the general finality of SkipGram is to learn word embeddings, its explicit goal remains to learn how to predict the context $c$ of a given word $w$. SkipGram uses a parametrized model (with parameters $\theta$) whose aim is to maximize the corpus probability:

where $p(c \mid w; \theta)$ is the probability that the context word $c$ was near $w$.

2.2. How does it learn?

The most successfull parametrized model for SkipGram to date is a neural network with one hidden layer $h$. The neural network can adequately model the conditional probability $p(c \mid x: \theta)$ using the softmax:

where $v_{c}$ and $v_{w} \in \mathbb{R}^{d}$ are vector representations for $c$ and $w$ respectively, and $C$ is the set of all available contexts.

SkipGram architecture

However, this approach is limited because as the size of our vocabulary increases, the normalization constant of the softmax needs to compute a growing number of terms $e^{v_{c’}\cdot v_{w}}$, $\forall c’ \in \text{vocabulary}$.

2.3. Learn faster with Negative sampling

Mikolov et al. introduce the negative sampling objective, which is much (much) faster to optimize than the classical softmax. The trick they use is that they instead aim to maximize the probabilities that all of the observations indeed came from the data:

See this tutorial paper for the full derivation equivalence. However, in this setting, a trivial solution (see below) can be obtained and leads to a non-injective representation (two identical vectors for two distinct words).

Non-injective representation from tutorial_paper:
Set $\theta$ such that $p(D = 1|w, c; \theta) = 1$ for every pair $(w, c)$. This can be easily achieved by setting $\theta$ such that $v_{c} = v_{w}$ and $v_{c} · v_{w} = K$ for all $v_{c}, v_{w}$, where $K$ is large enough number (practically, we get a probability of $1$ as soon as $K \approx 40$).

To palliate this issue, negative sampling introduces a generated dataset $D’$ made of incorrect pairs to “balance” the probabilities. This result in the negative sampling loss:

Using the sigmoid function $\sigma$, this is equivalent to:

We negate the above quantity and have our loss:

2.4. Select the Negative samples

For $k$ negative samples, the generated dataset $D′$ (i.e the vocabulary) is $k$ times larger than $D$, and for each $(w, c)$ in $D$ we construct $k$ samples $(w, c_{1}), . . . ,(w, c_{k})$, where each $c_{j}$ is drawn according to its unigram distribution raised to the $3/4$ power.

Indeed, the probability to randomly pick a word from a dataset is the count of the word’s occurrence divided by the total number of words in the dataset.

where $P(w_{i})$ is the probability to draw the word $w_{i}$ and $f$ is the functions that counts the number of occurrences of a given word in the dataset.

Mikolov et.al. state that they tried a number of variations on this equation, and the one which performed best was to raise the word counts to the 3/4 power. Therefore, the probability distribution becomes:

This distribution has the tendency to increase the probability for less frequent words and decrease the probability for more frequent words.

3. word2vec in python!

3.1. The class SkipGram

Our python model is defined by a class whose structure is the following:

class SkipGram:
    def __init__(self, sentences, ...):
        """
        - Set attributes
        - Create vocabulary
        - Hashing trick and subsampling
        - Negative sampling distribution
        """

    def train(self, batch_size = 128, ...):
        """
        - Retrieve in and out contexts (i.e. real and negative samples)
        - Train the model
        """

    def save(self, path):
        """ Pickle object """

    def load(path):
        """ Load object """

    def similarity(self, word1, word2):
        """ Compute cosine similarity """

3.2 Preprocessing is done in __init__

As the resulting SkipGram will be trained on a unique corpus, many tasks specific to the corpus will be done once within our SkipGram. In consequence, our __init__ method will serve four goals:

  1. Text preprocessing: We use a white space stemmer as a baseline in this work. Additionally, we remove punctuations as it oftentimes leads to duplicate of words (‘bye’ and ‘bye.’). We choose to use list comprehension motivated by this Quora question. It can be further optimized using a C based look-up tables. Finally, we remove digits.
def preprocess_line(line):
    lower = line.lower()
    punctuation = ''.join(c for c in lower if c not in string.punctuation)
    digits = ''.join([i for i in punctuation if not i.isdigit()])
    clean_line = digits.split()
    return(clean_line)
  1. Hyperparameters: We set the hyperparameters specific to the model (window_size, embedding_dimension…) as attributes and we add all remaining hyperparameters (epochs, stepsize…) to centralize them altogether.
# Basic attributes
self.window_size = window_size # number of surrounding words
self.min_count = min_count # remove low occuring word
self.negative_rate = negative_rate # number of negative samples
self.embedding_dimension = embedding_dimension
self.epochs = epochs
self.stepsize = stepsize
self.dynamic_window = dynamic_window # boolean
self.subsampling = None or 1e-5 # see below
  1. Create vocabulary: The vocabulary is a key component of the SkipGram model. Its main goal is to construct an integer indexing of the words (e.g. two dictionaries self.word2idx and self.idx2word). For convenience purposes, the indexes are sorted by the number of occurences. We use np.unique with return_counts = True to obtain the unique words of the corpus and their respective count. We save the number of occurences in a dictionary self.wordcount which will be useful for subsampling.
# Count words and create a sorted dictionary
unique, count = np.unique(np.array([x for sentence in sentences for x in sentence]), return_counts = True)
idx = np.where(count > min_count)
unique, count = unique[idx], count[idx]

# Word count
self.word2count = dict(zip(unique, count))
self.word2count = dict(sorted(self.word2count.items(), key=lambda kv: kv[1]))

# Retrieve vocabulary size after min count
self.vocab_size = len(self.word2count)

## Create mapping between words and index
self.idx2word = dict(zip(np.arange(0, self.vocab_size), self.word2count.keys()))
self.word2idx = {v:k for k, v in self.idx2word.items()}
  1. Corpus encoding: We convert the list of sentences by replacing each word by its index from word2idx. List comprehension leads to more efficient computations of words contexts and is lighter in terms of storage.
# Encode corpus
self.corpus_idx = [[self.word2idx[w] for w in sent] for sent in sentences]
  1. Negative sampling distribution is computed upstram for efficiency purposes. This results in word_distribution and the corresponding normalization_cte. It makes sense to integrate it in the __init__ as these solely rely on the occurences of each word word2count.
# Create distribution
self.normalization_cte = sum([occurence**0.75 for occurence in self.word2count.values()])
self.word_distribution = {k:v**0.75/self.normalization_cte for k, v in self.word2count.items()}

This distribution is only sampled during the training phase, in run_batch!

3.3. Retrieve the contexts

The basic idea behind computing context_word is to go over all the words in the corpus (much like one would read a corpus) and see which word is near the current word within a given window. At a given word in this “reading”, we retrieve its nearby words in python using:

def retrieve_context(w, window_size, encoded_sentence, dynamic_window = False):

    # Change to dynamic window
    if dynamic_window: window_size = np.random.randint(1, window_size+1)

    # List comprehension to retrieve the words
    context = encoded_sentence[max(w - window_size, 0) : w] + \
              encoded_sentence[w + 1: min(w + window_size + 1, len(encoded_sentence))]

    return(context)

3.4. The train method

The train method incorporates the three tasks of SkipGram coupled with Negative sampling:

  1. Retrieve the in-context(i.e. surrounding words)
  2. Draw the out-contexts with negative sampling distribution
  3. Run batch with target words labeled $1$ and their negative samples labeled $0$.

And because tasks like context retrieval and drawing negative samples can be done once at the beginning, we do it before the epochs, to lower computations time. Let’s initialize uniformly the weights:

w0 = np.random.uniform(-1, 1, size = (self.vocab_size, self.embedding_dimension))
w1 = np.random.uniform(-1, 1, size = (self.embedding_dimension, self.vocab_size))

In-contexts: We use python map operator instead of for loop. The in-contexts are computed using list comprehension (see previous section for more details).

# Context creation
contexts_corpus = map(lambda x: contexts_sentence(x, self.window_size, self.dynamic_window), self.corpus_idx)
# Flatten nested list
contexts_corpus = [item for sublist in contexts_corpus for item in sublist]

Out-contexts: The Negative sampling works by generating $k$ negative samples for each context_word. As for sampling, it is standard to proceed with np.random.choice. At first, they were drawn within each batch. This slow down the learning process immensely. Therefore, we draw all negative samples at once before the first epoch (with replace = True). In python, this translates to:

negative_samples = np.random.choice(list(self.word2idx.values()),
                                    size = (len(contexts_corpus), self.negative_rate * self.window_size),
                                    p=list(self.word_distribution.values()),
                                    replace = True)

Altogether we obtain the optimized learning procedure:

# In-contexts retrieval
# Negative sampling
## Repeat training on whole corpus self.epochs times
for epoch in range(0, self.epochs):
    ## For every word in the corpus
    for i, current in enumerate(current_words):
        w0, w1, ... = run_batch(self, current, contexts_corpus[i], w0, w1, ...)

3.5. The gradients

Learning is done with gradient descent on the weights $x = w^{0}$ and $y = w^{1}$ and the first step is to calculate the derivative of the loss regarding the output:

  • $y_{j\in J}$ are the embeddings for the in-context words $J$
  • $h$ is the output value of the hidden layer
  • $y_{j}$ are the labels of the word $w_{j}$ ($1$ if $w_{j}$ is the positive sample, and $0$ otherwise)

This is easy to compute because it is simply the error on the algorithm’s output for our batch.

Embeddings gradient

The next step is the derivative of the loss regarding the output vector of the word $w_{j}$:

Therefore the update equation for the output vector is:

Compared to the update equation given on the simple skipgram version, this update equation is much computationally efficient as it only has to be applied on the set of negative samples and the positive sample.

Input $\rightarrow$ Hidden weights

To backpropagate the error to the hidden layer and thus update the input vectors of words, we need to take the derivative of $E$ with regard to the hidden layer’s output.

Where $\mathcal{W}$ is the set of words in the negative and positive samples.

Finally we use the same w update equation as for the classic skipgram architecture.

I python, we can vectorize these gradient computations with:

def gradients_custom(target, prediction, current_word, context_words):
    # Compute error
    error = prediction - target

    # Exact gradients
    grad_w0 = np.sum(error*context_words, axis = 1)
    grad_w1 = np.outer(current_word, error)

    return(grad_w0, grad_w1)

3.6. Construct and run a batch!

While the the weights w0 and w1 are initialized prior the epochs loop, the whole embedding learning can be boiled down to a batch. Word2vec thereby learns by running (lots of) batches, with each batch consisting of the current word, contexts_word and corresponding negative_samples.

def run_batch(sg, current, contexts_word, negative_samples, w0, w1, epoch_error, sgd_count):
    # PREPARE BATCHE
    # FORWARD PASS
    # BACKWARD PASS
    return(w0, w1, epoch_error, sgd_count)

Preparing the batch: All we need are the in and out contexts (see negative_samples and contexts_word), because we know their respective labels. The negative_samples are drawn at each epoch (see 3.4.) and passed through

batch_contexts = contexts_word + list(negative_samples)
target = np.array([1 for ctxt in contexts_word] + [0 for i in negative_samples])

Forward pass: We retrieve the w0 of the current word and the embeddings w1 of the context words. We take the sigmoid of their dot product.

# Get embeddings and weights
current_word = w0[current,:]
context_words = w1[:, batch_contexts]
# Probabilities
output = expit(np.dot(current_word, context_words))

Backward pass: We compute the gradients as explained in section 3.0. and update the weights.

# Gradient computations
gradient_loss = gradients_custom(target, output, current_word, context_words)
# Update
w0[current,:] -= sg.stepsize * gradient_loss[0]
w1[:, batch_contexts] -= sg.stepsize * gradient_loss[1]

4. Improve Word2Vec

4.1. Dynamic window size

As a dynamic window size arguably leads to better results, we integrate this to our code using the attribute self.dynamic_window = True to the __init__ method. As for the actual computations, we use randint function from numpy. Altogether, this gives

if self.dynamic_window: win = np.random.randint(1, self.window_size + 1)
else: win = self.window_size

4.2. Effect of subsampling and rare-word pruning

Min count: Trying to learn contexts of rare words in the corpus is problematic for SkipGram, as there is not enough samples to train properly. And because there are less contexts to learn, this boosts the overall training speed. We retain words with at least self.min_count = 5 occurences.

Subsampling: Implemented as is, the frequent words such as ‘the’, ‘is’ undermines the ability of SkipGram to learn great embeddings. To tackle this issue, frequent words are down-sampled. The motivation behind this variation is that frequently occuring words hold less discriminative power. The underlying motivation is the effect of increasing both the effective window size and its quality for certain words. According to Mikolov et al. (2013), sub-sampling of frequent words improves the quality of the resulting embedding on some benchmarks.

For a given threshold $t$, we remove a word with frequency $f$ with probability:

frequencies = {word: count/self.total_words for word, count in self.word2count.items()}
drop_probability = {word: (frequencies[word] - subsampling)/frequencies[word] - np.sqrt(subsampling/frequencies[word]) for word in self.word2count.keys()}
self.train_words = {k:v for k, v in drop_probability.items() if (1 - v) > random.random()}
self.corpus_idx = [[self.word2idx[w] for w in sent if w in self.train_words.keys()] for sent in sentences]

Implementation note: Importantly, these words are removed from the text before generating the contexts (in __init__).

5. Experiments

5.1. Word similarity

Example of evaluation

5.2. Post-processing embeddings

Post-processing = PCA

5.3. Sentence similarity with BoW vectors

5.4. Cross-linguality

6. Future work

6.1. Character n-grams

This is motivated by these answers. See python implementation. This one seems more nice and efficient though.

6.2. Algebraic properties of the embeddings

7. Sources

Laisser un commentaire

Vous pourriez aimer

Spark introduction

1 minute de lecture

Mis à jour :

This lecture will be an abstract overview, we will discuss:

  • Spark
  • Spark vs MapReduce
  • Spark RDDs
  • Spark DataFrames

Hadoop

1 minute de lecture

Mis à jour :

When data gets too large to be dealt with in memory (most computers have up to 32 GB in RAM usually), it is possible to use a distributed system.

Link prediction

8 minute de lecture

Mis à jour :

In this lecture, we learn the basics of how to perform unsupervised link prediction and supervised ling prediction. We will overview the following techniques:

Link prediction

plus petit que 1 minute de lecture

Mis à jour :

Spreading through Network